Neurosymbolic Representation Learning

Deep Learning Systems

Deep Learning systems learn to solve all kinds of pattern recognition task by examples without human intervention. It is a machine learning technique that is currently utilized in most common image recognition, natural language processing (NLP) or speech recognition tasks. They usually require substantial amounts of data to return satisfactory performance levels.

When sufficient high-quality data are available, deep neural networks are successful in learning and reasoning by approximately representing data in the vector space. However, in practice, traditional deep learning is limited by out-of distribution data and demonstrated insufficient capacity in system generalization. Recently, it has become a hot topic within the NLP community how we can improve the reliability and performance of current deep learning approaches. 

Neurosymbolic Representation Learning

A word can have different meanings in different contexts. Humans can easily figure out the particular meaning of a word in a given context. But it is one of the hardest tasks for AI to select the correct meaning in a sentence, the so-called »word-sense disambiguation« (WSD). Its quality will affect the performance of all down-stream tasks, such as sentence understanding, question-answering, translation.

We research novel methods to precisely represent knowledge in the vector space, to promote the performance of neural networks beyond current state-of-the-art approaches. We were successful in developing a »neurosymbolic representation method« that precisely unifies vector embeddings as geometrical shapes into sphere embeddings, which inherit the features of explainability and reliability from symbolic structures (Dong, T., 2021).

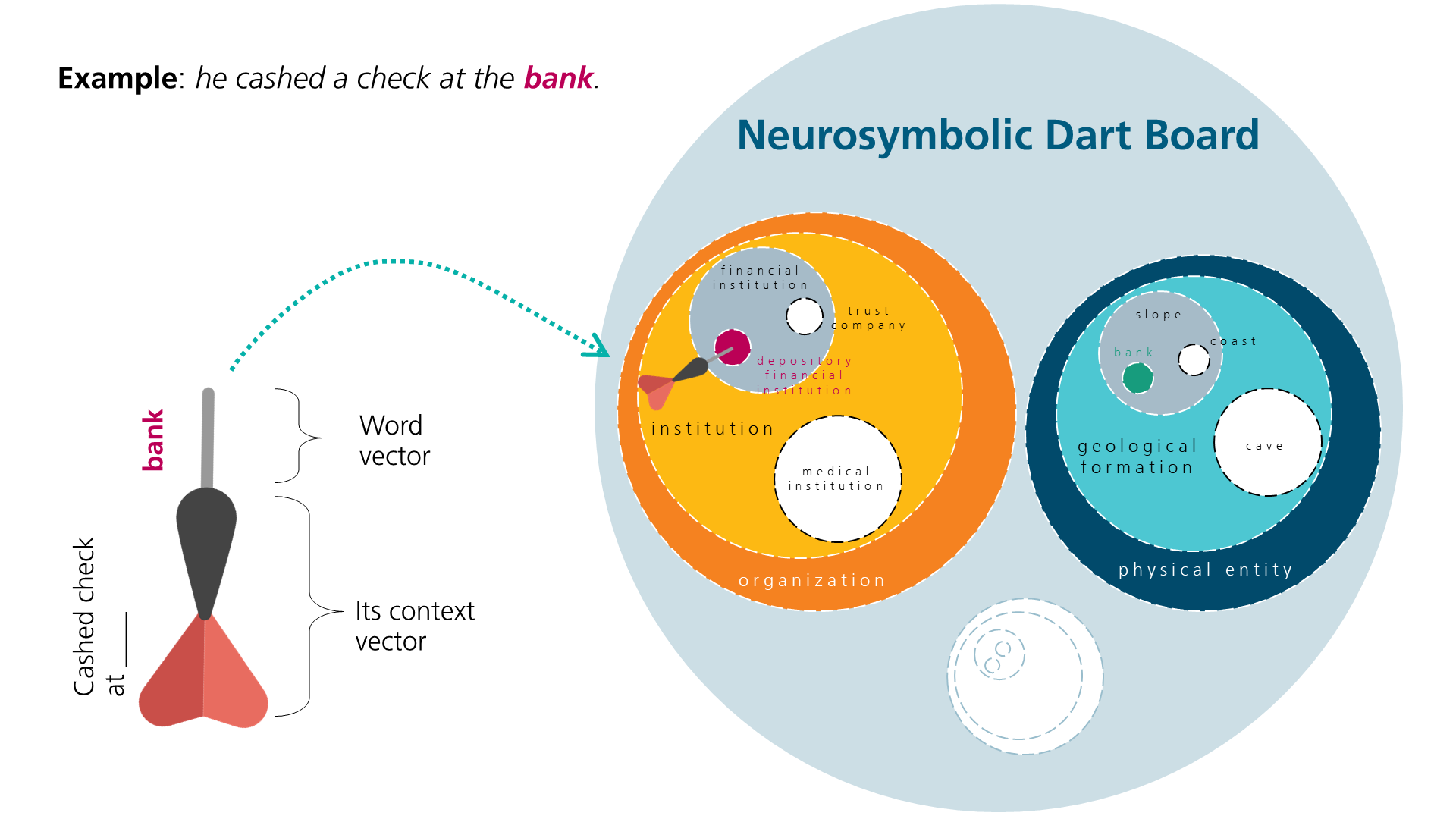
The Neurosymbolic Darter

We took existing deep learning structures and traditional artificial intelligence approaches and used our novel method for WSD-tasks. We precisely imposed the taxonomy of classes onto the vector embedding learned by the deep learning networks. This turns vector embeddings into a configuration of nested spheres, which resemble a dart board. Given a word and its context, we build a contextualized vector embedding of this word, as a »dart arrow«. Its word-sense is embedded as a sphere in the neurosymbolic dart board. This process works like shooting a dart arrow into a dart board. Hence, we named our neurosymbolic classifier prototype the `neurosymbolic darter'. 

Breaking the limits

Compared with traditional deep-learning methods, our method has several advantages:

(1)    It is much easier to hit a sphere, than hitting a specific point in the vector space, as it is the case with traditional deep-learning methods.

(2)    Explicit embedding of the taxonomy enhances the explainability of the results.

(3)    the configuration of nested spheres enables logic deduction among the taxonomy of word-senses.

Our experiments show that our »neurosymbolic darter« can break the performance ceiling of pure deep-learning neural-networks. Our neurosymbolic method can push the F1 score above 90%, which breaks the glass ceiling (80%) of pure deep-learning approaches to word-sense disambiguation. As previously mentioned, data availability and quality are often a bottleneck when it comes to returning satisfactory results with deep learning systems. Our novel method delivers better outcomes even when data is not sufficient or of lesser quality.